Q-Qプロットの作成 - ステップ解説＆R実装例

Q-Qプロットとは
Q-Qプロットの作り方
パーセンタイルを求める公式
Z scoreの求め方
Rコード
おまけ - Half Normal Plot
- 参考サイト

Q-Qプロットとは

Q-Qプロットとは、回帰分析の残差が正規分布に従うかをチェックする図であり、Rではqqnorm()で描くことができます（図1）。

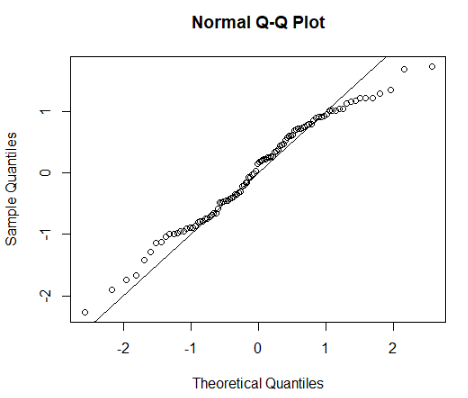
図1 Rで描いたQ-Qプロットの例。qqnorm(rnorm(100))で作成。

図1はrnorm()で生成した100個の点をプロットしたものであり、おおむねy=xの直線上に乗っていることが、正規分布に従うことを示しています。

このQ-Qプロットを残差に対してプロットして、「だいたい一直線なら回帰分析はＯＫ」、という非常にざっくりとしたイメージしか今まで持っていなかったので、このプロットがどのように作られているかを調べてみました。

Q-Qプロットの作り方

Q-Qプロットは、以下のフローで作ることができます。

■Q-Qプロットの作り方（図2）■

① パーセンタイルP_i=(i-0.375)/(n-2×0.375+1), i=1,2,...n（=データ数）を計算※1

② パーセンタイルP_iに対応する標準正規分布のパーセント点Z scoreを計算※2

③ データを昇順に並べる

④ ③のデータを縦軸に、②のZ scoreを横軸にプロットしてQ-Qプロットの完成

①のパーセンタイルの公式（※1）と、②のZ scoreの求め方（※2）については後述します。

図2はサイズn=10のデータ sample = (-0.463, -0.280, -0.414, 1.62, -0.72, -0.45, 0.01, 0.22, 0.19, -0.05) に対してQ-Qプロットを作図するフローを示したものです。

図2 sampleデータに対してQ-Qプロットを作成するフロー。
①公式を用いてパーセンタイルP_iの計算する。②正規分布において累積確率がP_iになるようなパーセント点(Z score)を計算する。③プロットしたいデータを昇順に並べる。④②のZ scoreと③のデータをプロットしてQ-Qプロットの完成。

パーセンタイルを求める公式

①パーセンタイルの公式（※1）について補足します。

データx_iに対するパーセンタイルとは、x₁~x_iがx全体に占める割合のことで、このパーセンタイルP_iの期待値は

$E[P_i]=i/(n+1)$

と書くことができます。xが一様分布に従う場合、順序統計量x(i)がベータ分布に従うことから上式を導出できます*1。xが正規分布に従う場合は修正を加えて

$E[P_i]=\frac{i-a}{n+2a-1}$

に対してa=0.375とすることで、パーセンタイルの期待値が計算されます。*2

Z scoreの求め方

次に、②Z scoreの求め方（※2）について説明します。

パーセンタイルP_iを求めたら、正規分布において累積確率がP_iになるような横軸の点ZがZ scoreとなります。図3左の累積分布では、P_i=0.84（縦軸）に対応するZ score（横軸）が1であることを示しています。図3右は全く同じことを確率密度関数を使って示したものですが、Z<1となる確率が0.84であることが分かります。

図3 パーセンタイルからZ scoreを求める様子。
左図は正規分布の累積分布において、縦軸がP_iとなるような横軸の値としてZ scoreを求めている。右図は正規分布の確率密度において、下側確率（Z<Z score）がP_iになるような横軸の値としてZ scoreを計算している。

Rコード

本記事で作成した自作のQ-Qプロットと、Rのデフォルトの関数であるqqnorm()を比較します。

#1.パーセンタイルの計算
percentlie <- (seq(10)-0.375)/(10-2*0.375+1)
#2.Z scoreの計算
zscore <- qnorm(percentlie, lower.tail = TRUE)

#今回プロットするデータの設定
set.seed(3)
#今回プロットするデータ10点
sample <- rnorm(10)
#3.データを昇順に並べる
plot(sort(sample), pch=16)

#Rの関数qqnorm()
qqnorm(sample, xlab = "", ylab="", pch=16, xlim=c(-2,2), ylim=c(-2,2))

#4. 2と3から自作のQ-Q plotを作成して重ね書き
par(new=T)
plot(zscore, sort(sample), col="red", pch=2, xlim=c(-2,2), ylim=c(-2,2))

#y=xの直線と凡例の追加
abline(a=0,b=1)
legend(x=-2,y=2, legend=c("qqnorm()", "self-made"), pch = c(16,2), col = c("black", "red"))

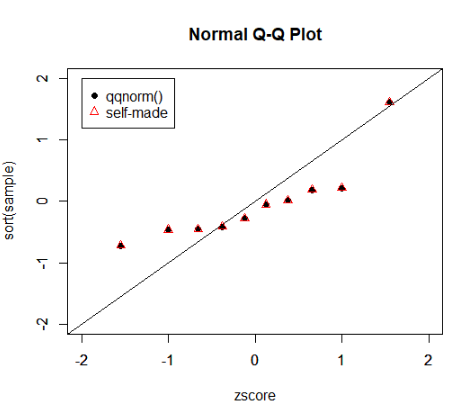
以下、上記のコードの出力結果です。自作のQ-Q plotとRが用意しているqqnorm()が一致していることを確かめられました！