
Half Normal Plotとは
Half Normal PlotとQ-Q Plotに似ていますが、Half Normal Plotはデータの絶対値を正規分布と比較したものになります。図1に例を示します。
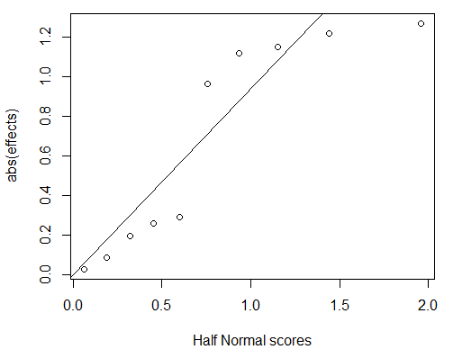
Q-Q Plotと同じように、Half Normal Plotもy=xの直線状におおむね乗っていれば、データが正規分布に従うことを意味しています。
実験計画法では、要因効果の絶対値に対してHalf Normal Plotを作成し、直線から外れている大きな効果を視覚的に判断するために用います。
要因数が多い場合、残差の自由度がゼロになってしまうと分散分析ができませんが、そのような場合でも、Half Normal Plotを使って、ほかの要因より効果が大きな要因を抽出することが可能です。
以下では、Half Normal Plotの作り方を説明しますが、基本となる考え方はQ-Q Plotなので、先にQ-Q Plotの理解をしていただければと思います。
Half Normal Plotの作図方法
図2にHalf Normal Plotの作成フローを示します。
① パーセンタイルPi=(i-0.5)/n, i=1,2,...n(=データ数)を計算
② パーセンタイルPiに対応するHalf Scoreを計算。正規分布に従うZに対して、P(|Z|<Half Score)=Piとなる※
③ データの絶対値を昇順に並べる
④ ③のデータの絶対値を縦軸に、②のHalf Scoreを横軸にプロットしてHalf Normal Plotの完成
※②のHalf Scoreの求め方については後述。

Half Scoreの求め方
※②のHalf Scoreは、①で求めるパーセンタイルPiに対して
P(|Z|<Half Score) = Pi
となります。ここで、Zは標準正規分布に従う確率変数です。
具体例を用いてHalf Scoreを計算してみましょう。今、図2中①で求めたパーセンタイルPi=4=0.453に対して、Half Scoreを計算してみます。
パーセンタイル=下側確率ですから、0.453は下図の青色で塗りつぶした領域の面積になります。
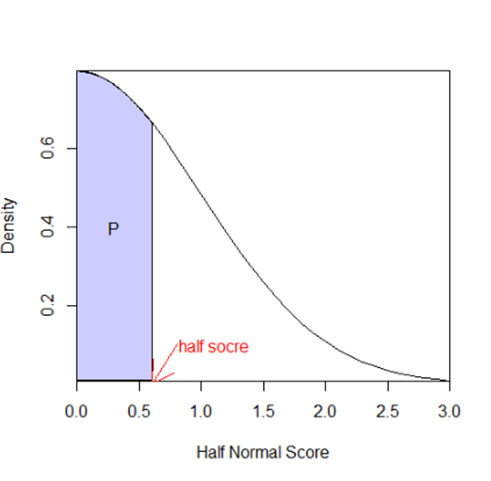
上の図3の確率分布は、正規分布を折り返してできたものなので、もとの正規分布に戻すと図4のようになります。図4の青色の部分が図3中の確率Pと一致します。
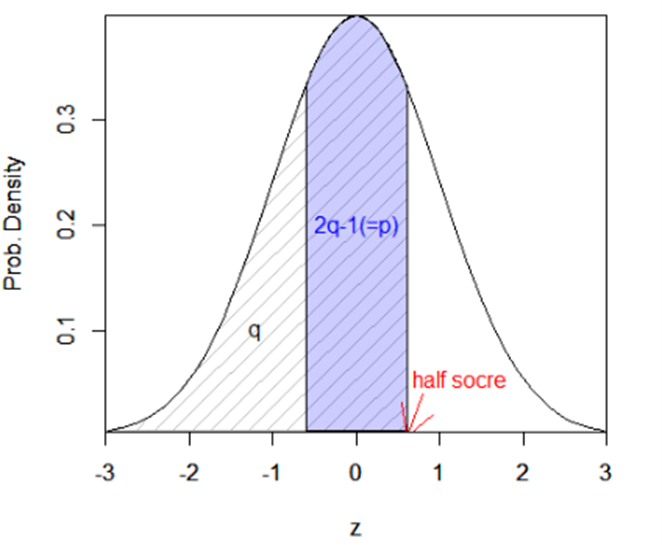
図4の正規分布において斜線部分の面積をqと置くと、p=1-(1-q)*2=2q-1の関係があります。したがって、q=(p+1)/2でqを求めて、正規分布の下側確率がqとなるパーセント点がhalf scoreとなります。
Rコード
以下のコードでHalf Normal Plotを作成しました。
p <- (seq(10)-0.5)/10#1. パーセンタイル計算 q <- (p+1)/2#2-1.正規分布に戻したときの下側確率 half_score <- qnorm(q)#2-2. Half Scoreの計算 set.seed(3)#今回プロットするデータの設定 sample <- rnorm(10)#今回プロットするデータ10点 plot(sort(abs(sample)), pch=16)#3.データの絶対値を昇順に並べる plot(half_score, sort(abs(sample)), col="red", pch=2, xlim=c(0,2.1), ylim=c(0,1.3), xlab="Half Score", ylab="abs(sample)")#4.Half Normal Plot abline(a=0,b=1)

黒●: halfnorm()はlibrary"daewr"の関数
ちなみにですが、図5の黒●はdaewrというlibrayのhalfnorm()関数で作成したもので、ちゃんと一致していることが確かめられました。
関数halfnorm()については、以下の記事でも紹介しています。