配合計画まとめ

配合計画とは

配合計画は比率に関する実験計画です。例えば、材料A, B, Cを用いてある製品を作製するとき、それらの比a:b:cに対する特性yの応答を知りたい場合に使用できます。

3つの因子がある配合計画は、図1のようなコンタ―図によって特性の応答を表すことが出来ます。この図を見れば、例えば(a,b,c)=(1/3, 1/3, 1/3)の時、特性yは14~16である、というようなことが見て取れます。

図1. 3元系の配合実験によって得られるコンタ―図

配合計画が他の実験計画と異なるのは、ある一つの因子Aを増加させたとき、対応して別の因子Bが減少する、というような関係があること。つまり、因子どうしは独立でありません（他の実験計画では因子どうしは独立に推定しようとします）。配合計画の本質的な因子は、要因そのものではなく、要因間の"比率"なのです。

3元系の配合計画でよく使われる図

図1にも示したように、3元系の配合計画では3元系図（ternary plot）が良く使用されます。本記事でも、この3元系図を使いますので、はじめに図の読み方を説明します。

図2に、3元系図の読み方を示しました。

図2. 3元系図の読み方

図2で、星形に示した実験点のA, B, Cの比率(a, b, c)を読み取りたいとします。はじめに、3つの頂点のそれぞれに、a=1, b=1, c=1の線を引くと分かりやすいです。その線と平行に、対象の実験点から各辺へと線を伸ばします。すると、(a,b,c)=(1/6, 1/6, 2/3)のように比率を読み取ることが出来ます。

配合計画の作成方法

配合計画には以下のような種類があります。

1. シンプレックス格子（図3）
2. セントロイド（図4）
3. 軸上点（図5）
4. 最適計画
5. 空間充填

図3～5に一般的な配合計画の実験点を示しました。最適計画や空間充填による配合計画の作成は、実験回数が限られていたり、配合に制約がある場合（たとえばＡは必ず0.5以上含むなど）に使用するのが効率的です。

また、前半は回数の少ないシンプレックス格子によって実験を実施し、実験点が足りなければ、セントロイドや軸上点によって計画を拡張する、という方法もアリです。

図3. シンプレックス格子

図4. セントロイド

図5. 軸上点

配合計画の分析方法

配合計画の分析は、他の実験計画法と若干異なります。モデルに高次の項を含むことが多いですが、例えば3元系の2次モデルの場合には、以下のモデルを使用します。

ここで、x12のような項は配合計画の2次モデルには含まれません。なぜなら、例えばx3を固定したとき、

なので、x1x2がx1（あるいはx2）の2乗効果を意味するからです。また、モデル式には切片項もありません。なぜなら、すべての因子の値が0の場合は存在しないからです。

以上のように、配合計画のモデル式は他の実験計画で使用するモデル式とは若干違います。

以下では、図6に示す3元系の配合実験とその結果（実験点の横に表記）を用いて、分析を行いました。

図6. 3元系（x1, x2, x3）の配置計画とその結果（実験点の横に表記）

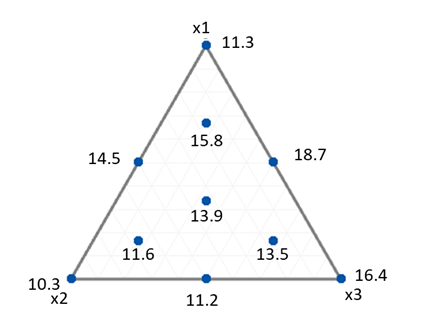
 図６の計画とその結果をもとに、先ほどの2次モデルを用いた回帰分析を行うと、

となりました。これをコンタ―図として図6にプロットすると、図7のようになります。

図7. 応答yのコンタ―図（図６に重ねたもの）

最後に

本記事では、配合計画の例として3元系のみを扱いましたが、もちろん要因の数は何個でもできます。ただ、4元系以上となると実験点の表示が難しくなるので、工夫が必要です（4元系の場合は、四面体を用いて実験点を表現することができます）。

また、配合に含まれない因子と、配合に含まれる因子を組み合わせて計画を作成することもできます。それについては、また別の記事でまとめたいと思います。